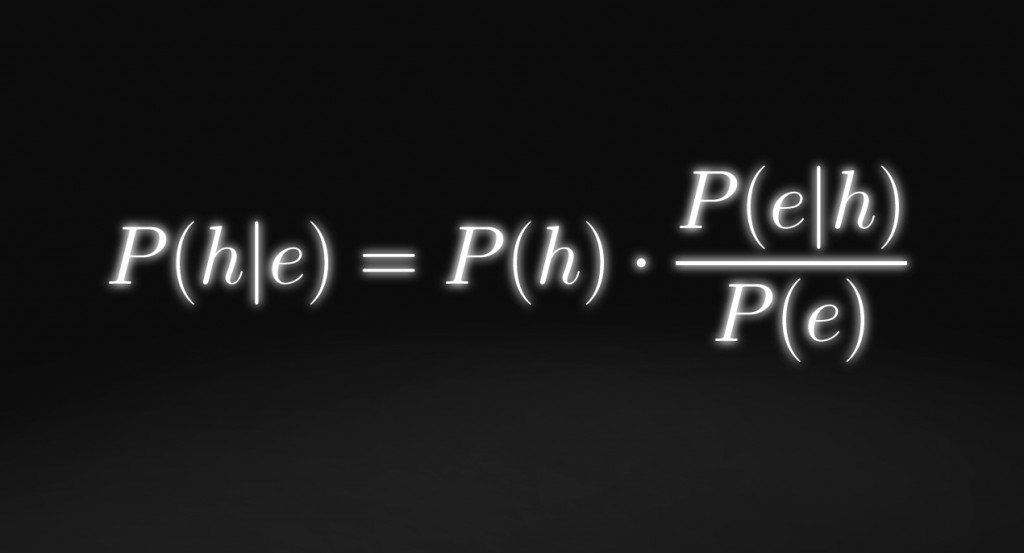Wahrscheinlichkeit wird oft als etwas vorgestellt, das objektive Tatsachen beschreibt, zum Beispiel über Würfel oder Karten. Man spricht dann von der Tatsache, dass die Wahrscheinlichkeit, mit einer fairen Münze drei Mal hintereinander „Kopf“ zu werfen, 1/8 beträgt. Im Kontext der Rationalitätsdiskussion beschreibt Wahrscheinlichkeit jedoch nicht objektive Tatsachen über Glücksspiel-Artefakte, sondern die Glaubensgrade eines Subjekts. Wahrscheinlichkeitstheorie ist dementsprechend nicht als Rechenmethode zur Lösung mathematischer Probleme mit Gegenständen in der Welt zu verstehen, sondern als Anleitung zur rationalen Aktualisierung von Glaubensgraden. Diese Perspektive nennt man die subjektivistische oder Bayesianische Wahrscheinlichkeitstheorie. Um uns die Bedeutung dieser Perspektive vor Augen zu führen, können wir uns folgende Situation vorstellen:

Ich möchte wissen, ob ich an einer bestimmen Krankheit leide, die bei 1% der mit mir vergleichbaren Menschen auftritt. Die zu testende Hypothese h ist also, dass ich an dieser Krankheit leide. Es gibt einen einfachen Test, der diese Krankheit ausnahmslos erkennt – doch in 10% der Fälle liefert er falsch positive Resultate, d.h. er verzeichnet eigentlich gesunde Menschen als krank. Ich mache den Test und erhalte ein positives Resultat – die Evidenz e, die darauf hinweist, dass ich die Krankheit habe. Was ist nun die Wahrscheinlichkeit, dass ich die Krankheit wirklich habe?

Die folgende Überlegung liegt nahe: Der Test ist in 10% der Fälle unzuverlässig, also muss die Antwort 90% sein; mein Glaubensgrad, dass ich wirklich an der Krankheit leide, sollte demnach 0.9 betragen. Doch das ist völlig falsch. Die tatsächliche Wahrscheinlichkeit, dass ich krank bin, liegt bei kaum mehr als 9%.

Weshalb ist das so? Gehen wir einen Schritt zurück und rollen das Problem auf ganz allgemeiner Ebene noch einmal auf: Eine Beobachtung liefert uns neue Informationen – die Evidenz e – und wir möchten deren Bedeutung für eine Erklärung oder Hypothese h erörtern. Das Prinzip der Konditionalisierung besagt aber, dass nach der Beobachtung der relevanten Evidenz unsere neue Einschätzung der Wahrscheinlichkeit der Hypothese  denjenigen Wert annehmen sollte, der unserer alten Einschätzung der Wahrscheinlichkeit der Hypothese gegeben der Evidenz entspricht. Es sagt uns allerdings nichts darüber, woraus sich diese alte Einschätzung zusammensetzen sollte. Eine einfache, aber geschichtsträchtige Gleichung hilft uns hier weiter:

Diese Gleichung ist als das Bayestheorem bekannt und ist nach dem Reverend Thomas Bayes benannt, der sie im 18. Jh. herleitete. Sie stellt dar, wovon die Wahrscheinlichkeit einer Hypothese h – gegeben der Evidenz e – abhängen sollte.

Das Bayestheorem sagt uns nun, dass:

Das bedeutet, dass die alte Einschätzung der Hypothese gegeben der Evidenz zu bestimmen ist, indem wir die alte Wahrscheinlichkeit der Hypothese multiplizieren mit der alten Wahrscheinlichkeit der Evidenz gegeben der Hypothese dividiert durch die alte Wahrscheinlichkeit der Evidenz. Zusammen implizieren das Prinzip der Konditionalisierung und das Bayestheorem aber:

Wir können diese Gleichung auffassen als ein Rezept, um unsere alten Glaubensgrade in neue umzuwandeln, wenn wir neue Informationen erhalten. Dieses Rezept sagt uns, dass wir unsere alte Hypothesenwahrscheinlichkeit mit dem Bruch auf der rechten Seite multiplizieren sollen (mit der Wahrscheinlichkeit der Evidenz gegeben der Hypothese dividiert durch die Wahrscheinlichkeit der Evidenz überhaupt).

Was bedeutet das? Nun, dieser Bruch auf der rechten Seite entspricht nur einem Wert über eins, wenn der Zähler grösser ist als der Nenner – wenn grösser ist als . Das wiederum bedeutet, dass die Hypothesenwahrscheinlichkeit nur erhöht wird (also mit einer Zahl über eins multipliziert), wenn die Wahrscheinlichkeit der Evidenz gegeben der Hypothese grösser ist als die Wahrscheinlichkeit der Evidenz überhaupt. Genauer: Die Gleichung sagt uns, dass wir unseren Glauben an die Hypothese gerade in dem Masse erhöhen sollen, in dem  grösser ist als . Und das heisst nichts anderes, als dass die Hypothese bestätigt wird, wenn sie erfolgreich etwas voraussagt, das ansonsten unerwartet wäre.

Das Bayestheorem ermöglicht es uns zu sehen, weshalb eine Hypothese mehr Glaubwürdigkeit durch die Beobachtung ihrer überraschenden Konsequenzen erhält als durch die Beobachtung von Konsequenzen, die wir ohnehin – also unabhängig von der Hypothese – erwarten. Je wahrscheinlicher eine Beobachtung ist, um so geringer ist deren Aussagekraft. Unser Gehirn ist aber nicht darauf ausgelegt, diese Unterscheidung zu treffen. Stattdessen neigen wir zur Überbewertung von Beobachtungen, die unsere bestehende Meinung bestätigen.

Was das Bayestheorem ebenfalls veranschaulicht – und damit kommen wir zu unserem anfänglichen Problem zurück – ist die Wichtigkeit der vorausgehenden Wahrscheinlichkeit (prior probability) der Hypothese: Wenn wir ermessen wollen wie wahrscheinlich eine Hypothese im Lichte gewisser Daten ist, müssen wir dem Bayestheorem zufolge fragen: Wie wahrscheinlich ist es, dass sich die Evidenz der Wahrheit der Hypothese verdankt?

Das ist nicht gleichzusetzen mit der Wahrscheinlichkeit, dass wir die Evidenz e beobachten würden, wenn die Hypothese wahr wäre – diese Wahrscheinlichkeit können wir einfach mit formulieren. Aber um herauszufinden wie wahrscheinlich es ist, dass die Evidenz e kraft der Hypothese h zustande gekommen ist, müssen wir nicht nur  betrachten, sondern auch, wie wahrscheinlich die Hypothese h selbst ist. Denn dass e durch h zustande gekommen ist, kann auch sehr unwahrscheinlich sein, wenn  sehr hoch ist, solange  sehr tief ist. Die Wahrscheinlichkeit, dass ich in diesem Moment Harfenklänge vernehmen würde, wäre sehr hoch, wenn eine Schar musikbegeisterter Elfen jetzt unter meinem Fenster stünde. Aber die Wahrscheinlichkeit dieser Hypothese ist äusserst gering; und das muss ich beachten, wenn ich die Wahrscheinlichkeit davon kennen möchte, dass e durch die Wahrheit von h zustande gekommen ist. Wir müssen die vorausgehende Wahrscheinlichkeit der Hypothese miteinbeziehen.

Wenden wir dies nun auf unser anfängliches Beispiel an. Ich will wissen wie wahrscheinlich die Hypothese h ist, dass ich an einer bestimmten Krankheit leide. Nun habe ich ein positives Testresultat, die Evidenz e, bekommen. Wie wir wissen, können wir bei der Beobachtung von e unsere aktualisierte  bei der vorherigen  ansetzen. Und das Bayestheorem lässt uns diese berechnen, indem wir unsere  multiplizieren mit  durch .

Zwei dieser Wahrscheinlichkeiten sind einfach zu bestimmen.  war in obigem Beispiel 1%, und  ist 1, da der Test die Krankheit immer entdeckt, wenn sie vorhanden ist. hingegen ist etwas komplizierter: Was ist die Wahrscheinlichkeit eines positiven Resultats bei einer zufälligen Person? Nun, die 1% der Bevölkerung, die tatsächlich an der Krankheit leiden, werden sicher positive Resultate haben; und die anderen 99% werden 10% falsch positive Resultate liefern – was eine Summe von 10.9% ergibt. Somit ist

Meine  sollte also knapp über 9% betragen.

Es lässt sich auch so veranschaulichen: Wenn 1000 Leute den Test machen, werden 10 ein positives Resultat erhalten, weil sie krank sind – aber 99 gesunde Leute werden falsch positive Resultate erhalten! Ein positives Resultat sagt mir also nur, dass ich mit einer Wahrscheinlichkeit von 10/109 ≈ 0.0917 an der Krankheit leide.

Die Tendenz, die Bedeutung solcher Tests zu überschätzen, nennt man einen Prävalenzfehler oder Base-Rate-Fehlschluss. Sie beruht auf der Missachtung der (oft entscheidenden) vorausgehenden Wahrscheinlichkeit, an einer Krankheit zu leiden (ihre Prävalenz oder Base-Rate). Es ist ein äusserst verbreiteter Fehler. Wenn wir eine Situation antreffen, in der Hinweise auf eine bestimmte Hypothese hindeuten, beurteilen wir oft die Wahrscheinlichkeit der Hypothese nur ausgehend davon, wie gut die Hinweise zur Hypothese passen, und missachten dabei die vorausgehende Wahrscheinlichkeit der Hypothese.

Das Bayestheorem ist wichtig, weil es beschreibt, was eine Beobachtung zu einem Beleg macht, und in welchem Mass er als Beleg zu gewichten ist. Wenn wir neue Daten erhalten, erfolgt die Stärkung oder Schwächung unserer Hypothesen nach Bayesianischen Regeln. In diesem Sinne kann die wissenschaftliche Methode selbst als ein Spezialfall des Bayestheorems konzipiert werden. Das Theorem zeigt uns, wie viel Arbeit eine gegebene Beobachtung auf der Waage unserer Überzeugungsgrade leisten kann und soll. Deshalb redet man in den kognitiven Wissenschaften von Bayesianischen Denkern. Ein Bayesianischer Denker ist nichts anderes als ein rationaler Denker.