Updating: Das rationale Aktualisieren von Glaubensgraden
Unter dem Gesichtspunkt der Wahrscheinlichkeitstheorie haben wir in anderen Artikeln zwei Bedingungen für Rationalität identifiziert: Das Dutch-Book-Argument impliziert, dass rationale Glaubensgrade kohärent sein müssen (d.h. den Axiomen der Wahrscheinlichkeitstheorie entsprechen müssen); und das „Principal Principle“ impliziert, dass sie mit den objektiven Wahrscheinlichkeiten übereinstimmen sollten, wann immer solche vorhanden sind. Nun können wir eine dritte Bedingung einführen: Rationale Akteure sollten konditionalisieren, wann immer sie neue Informationen erhalten.
Um zu verstehen, was das bedeutet, führen wir zuerst den Begriff der bedingten Wahrscheinlichkeit ein, und formulieren anschliessend das Prinzip der Konditionalisierung.
Bedingte Wahrscheinlichkeiten
Die bedingte Wahrscheinlichkeit von p gegeben q – geschrieben: – ist die Wahrscheinlichkeit von p unter der Annahme, dass q. Sie lässt sich wie folgt messen:
Wenn wir die Wahrscheinlichkeiten als Flächen darstellen (in einem sogenannten Venn-Diagramm), entspricht die bedingte Wahrscheinlichkeit dem Verhältnis der Schnittwahrscheinlichkeit von p und q (geschrieben: ) zur Wahrscheinlichkeit von q – also dem Verhältnis zwischen der Fläche, in der sich p und q überlappen, und der Fläche von q.

So können wir zum Beispiel die bedingte Wahrscheinlichkeit erörtern, dass ich mit einem fairen Würfel eine gerade Zahl erhalte – aber unter der Bedingung, dass die Zahl grösser ist als drei. Das können wir schreiben als P(gerade | grösser als drei), und wir berechnen es wie folgt:
P(gerade & grösser als drei) / P(grösser als drei)
Dieser Bruch repräsentiert die Wahrscheinlichkeit einer geraden Zahl unter den Ergebnissen, die grösser sind als drei. Und er beträgt 2/3, denn: Die Wahrscheinlichkeit eines Ergebnisses, das gerade und grösser als drei ist (vier oder sechs), beträgt 2/6; die Wahrscheinlichkeit irgendeines Ergebnisses, das grösser ist als drei (vier, fünf oder sechs), beträgt 1/2; und 2/6 durch 1/2 ergibt 2/3.
Konditionalisierung
Angenommen, ich habe folgende rationalen Glaubensgrade:
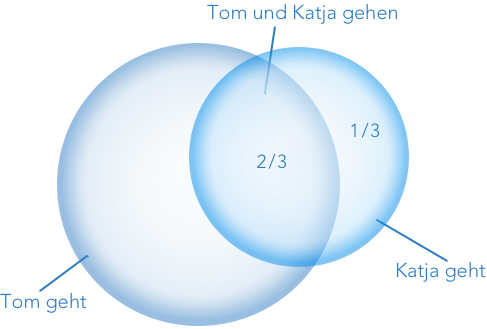
P(Tom geht an die Party) = 1/2
P(Tom geht an die Party | Katja geht an die Party) = 2/3
Nun erfahre ich, dass Katja an die Party geht. Was sollte jetzt mein Glaubensgrad sein, dass Tom geht?
Die Antwort ist klar – 2/3. Wenn es zuvor richtig war zu denken, dass die bedingte Wahrscheinlichkeit, dass Tom geht, gesetzt, Katja geht, 2/3 beträgt, und sich nun herausstellt, dass Katja geht, dann folgt daraus, dass Toms unbedingte Wahrscheinlichkeit auf 2/3 gestiegen ist.
Stellen wir uns das anhand eines Venn-Diagramms vor: Wir wissen, dass wir uns innerhalb der Venn-Diagramm-Fläche für „Katja geht an die Party“ befinden. Und wir haben bereits beschlossen, dass der Anteil dieser Fläche, der sich mit „Tom geht an die Party“ deckt, 2/3 beträgt. Also muss es nun rational sein, einen unbedingten Glaubensgrad von 2/3 zu haben, dass Tom geht.
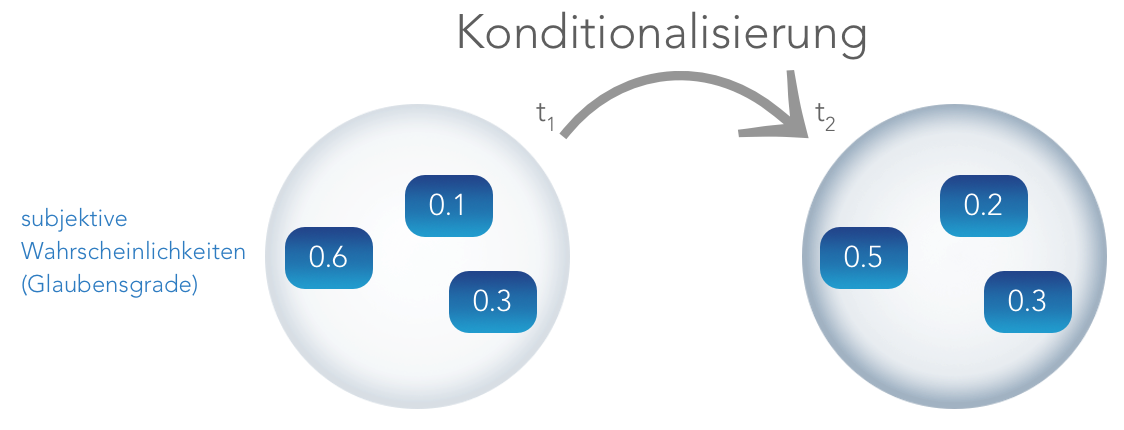
Eine derartige Anpassung von Glaubensgraden bezeichnet man als Konditionalisierung. Wir können nun folgendes Rationalitätsprinzip formulieren:
Das Prinzip der Konditionalisierung
Wenn mein alter bedingter Glaubensgrad gleich
ist, und ich erfahre, dass q, sollte ich meinen neuen Glaubensgrad für p,
, mit
gleichsetzen.
Wichtig ist hier, dass q alles repräsentiert, was ich in Erfahrung bringe. Das Prinzip funktioniert nicht, wenn q nur einen Teil meines neuen Wissens darstellt. Nehmen wir an, ich erfahre nicht nur, dass Katja an die Party geht, sondern auch, dass Tina mitkommt; nehmen wir weiter an, dass ich schon immer gedacht habe, dass Tom wohl kaum an die Party geht, wenn sowohl Katja als auch Tina gehen (ich rechnete ursprünglich mit einer tiefen bedingten Wahrscheinlichkeit (Tom geht | Katja und Tina gehen), obwohl
(Tom geht | Katja geht) 2/3 betrug). Weil ich mehr erfahren habe als nur, dass Katja geht, ist es keine gute Idee mehr, Tom eine Wahrscheinlichkeit von 2/3 zuzuteilen. Ich befinde mich sozusagen nicht nur in Katjas Venn-Diagramm, sondern bereits in dem Teil, in dem Tina auch geht; und der Anteil dieser Fläche, in dem Tom auch geht, ist sehr klein.
Das Prinzip der Konditionalisierung ist nicht einfach eine Konsequenz des Dutch-Book-Arguments für Kohärenz. Letzteres zeigt nämlich, dass die Axiome der Wahrscheinlichkeitstheorie zu jedem gegebenen Zeitpunkt von meinen Glaubensgraden respektiert werden sollten. Das Prinzip der Konditionalisierung hingegen zeigt, wie ich meine Glaubensgrade als Reaktion auf neue Information anpassen sollte. Es zeigt mir, wie ich alte Glaubensgrade (…) durch neue Glaubensgrade
(…) ersetze. Vor Dutch-Book-Argumenten bin ich schon gefeit, solange
(…) und
(…) für sich genommen jeweils kohärent sind; das Prinzip der Konditionalisierung liefert mir darüber hinaus noch Angaben dazu, wie diese verschiedenen Glaubensgrade zusammenhängen sollten.
Serie: Rationalität & Wahrscheinlichkeitstheorie
- Warum jede Handlung eine Wette ist
- Das Dutch-Book-Argument: Weshalb Kohärenz rational ist
- Subjektive und objektive Wahrscheinlichkeit
- Updating: Das rationale Aktualisieren von Glaubensgraden
- Das Bayestheorem und der Base-Rate-Fehlschluss
